World's Hardest Easy Geometry Problem

Using only elementary geometry, determine angle x. Provide a step-by-step proof.

You may use only elementary geometry, such as the fact that the angles of a triangle add up to 180 degrees and the basic congruent triangle rules (side-angle-side, etc.). You may not use trigoomery, such as sines and cosines, the law of sines, the law of cosines, etc.

This is the hardest problem I have ever seen that is, in a sense, easy. It really can be done using only elementary geometry. This is not a trick question.

Here is a very small hint. Here is a small hint. These hints are not spoilers.

There is a review of everything you need to know about elementary geometry below.

Remember to provide a step-by-step proof. There are tips for writing proofs below.

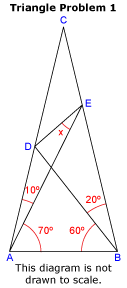
World's Second-Hardest Easy Geometry Problem

Using only elementary geometry, determine angle x. Provide a step-by-step proof.

This is a variation of the problem above. This is also a very hard problem that is, in a sense, easy.

Here is a very small hint. Here is a small hint. These hints are not spoilers.

Sorry, but I'm not giving the answer nor the proof here. You will just have to work on it until you either solve it or are driven insane. If you email me at k.enevoldsen@wlonk.com, I may give you a bigger hint (if I feel like it). If you think you have solved it, you can ask me if your answer is correct, but please also tell me how you got the answer. The proof may be written informally, but you need to tell me all the steps, or at least the key steps, in your solution. It is helpful if you also send me a diagram. Try to persuade me that you are not just guessing. I have additional small, medium, and large hints, but you must first show your efforts to convince me that you have struggled valiantly.

Please don't search the the web for the answer — that's cheating. You will only deprive yourself of many hours of delicious frustration. Of the proofs posted on other websites, some are valid proofs and some are not.

I did not invent these problems. After I first read problem 1, I worked on it for many hours over several days before I eventually figured it out. A couple of years later I came back to the problem, but I had forgotten my proof. It took me many hours to figure it out again! Problem 2 also took me many hours to solve.

How hard are these problems? Any teenage student can understand the proof, but very very few are able to discover the proof on their own. Of the people who have emailed me (more than a thousand), fewer than five percent (mostly math professionals and college students) have provided valid proofs without significant hints. (The hints given above are not significant hints.)

Based on my emails, most people who think they have found a proof are wrong. Most do not even have the correct answer for angle x. Of those that have the correct answer, the proofs they send me are usually wrong (incorrect or incomplete). People who say "it only took me a few minutes" almost never have a valid proof.

These problems have been published in many places. Problem 2 first appeared here: Langley, "A Problem", Mathematical Gazette, 1922. Dr. Gary Gruber says his high school teacher showed him problem 1 in about 1955. Tom Rike says problem 1 first appeared in print here: Harry Schor, The New York State Mathematics Teachers' Journal, 1974. It also appeared here: "Problem 134", Eureka (now Crux Mathematicorum), 1976. Dr. Gruber popularized problem 1 in several papers (such as "The Genius Test") which appeared in newspapers throughout the 1990s (Universal Press Syndicate and Los Angeles Times Syndicate). That's where I discovered it.

Notice that I call this the "world's hardest easy geometry problem", not the "world's hardest geometry problem". The world's hardest geometry problem would be something really hard, like the Poincaré conjecture.

Elementary Geometry

Here is everything you need to know to solve the above problems.

Lines and Angles

When two lines intersect, opposite angles are equal and the sum of adjacent angles is 180 degrees.
When two parallel lines are intersected by a third line, the corresponding angles of the two intersections are equal.

Triangles

The sum of the interior angles of a triangle is 180 degrees.
An isosceles triangle has two equal sides and the two angles opposite those sides are equal.
An equilateral triangle has all sides equal and all angles equal to 60 degrees.
A right triangle has one angle equal to 90 degrees.
Two triangles are called similar if they have the same angles (same shape).
Two triangles are called congruent if they have the same angles and the same sides (same shape and size).

SAS (Side-Angle-Side): Two triangles are congruent if two pairs of sides of the two triangles are equal, and the included angles are equal.
SSS (Side-Side-Side): Two triangles are congruent if three pairs of sides of the two triangles are equal.
ASA (Angle-Side-Angle): Two triangles are congruent if two pairs of angles of the two triangles are equal, and the included sides are equal.
AAS (Angle-Angle-Side): Two triangles are congruent if two pairs of angles of the two triangles are equal, and a pair of corresponding non-included sides are equal.
AA (Angle-Angle): Two triangles are similar if two pairs of angles of the two triangles are equal.

Tips for Writing Proofs

Proofs may be written informally using plain English. Just be sure to include all the steps in your reasoning, or at least all the key steps. Providing a diagram is very helpful but not required. You can draw a diagram on the computer or you can draw it on paper and then scan it or photograph it with a digital camera.

Please number your steps. This makes it easy for both writer and reader to talk about the steps.

Name each point you use with a letter (ex., say "point A" or simply "A"). Identify lines with two letters (ex., say "line AB" or simply "AB"). Identify triangles with three letters (ex., say "triangle ABC" or "tri ABC" or "△ABC" or simply "ABC"). Identify angles with three letters, vertex in the middle (ex., say "angle ABC" or "ang ABC" or "∠ABC" or simply "ABC").

If you don't provide a diagram, you will need to describe the named points with words (ex., say "the intersection of AE and DB is G"). Even if you provide a diagram, you must define with words each new line that you draw, in order (ex., say "Draw a line through C perpendicular to AB intersecting AB at H").

Justify all key steps (ex., say "AC=BC because ABC is isosceles"). You may omit the justification when simply "chasing angles" — calculating angles based on any of these simple rules: triangle angles sum to 180, supplementary angles sum to 180, opposite angles are equal.