Twelve-Tone Musical Scale
Why does the standard musical scale (in Western music) have twelve notes (counting both the white and black keys on the piano)? Why not ten or fifteen or twenty?
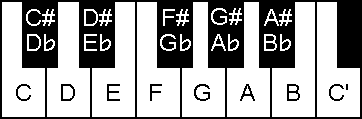
To answer this question, we first need some background information. A note's pitch or frequency is measured in cycles per second; for example, A' is 440 cycles per second. The distance between two notes, measured as the ratio of their pitches, is called an interval. If the interval between two notes is a ratio of small integers, such as 2/1, 3/2, or 4/3, they sound good together — they are consonant rather than dissonant. People prefer musical scales that have many consonant intervals.
There is no absolutely definitive list of consonant intervals because the concept of consonance involves subjective aesthetic judgment. However, the following seven pure intervals, smaller than or equal to an octave (2/1) and larger than unison (1/1), are commonly considered to be consonant.
Basic Consonant Intervals
| Ratio | Interval | Harmonic Inverse |
|---|---|---|
| 2/1 | octave | 1/1 |
| 3/2 | perfect fifth | 4/3 |
| 4/3 | perfect fourth | 3/2 |
| 5/3 | major sixth | 6/5 |
| 5/4 | major third | 8/5 |
| 6/5 | minor third | 5/3 |
| 8/5 | minor sixth | 5/4 |
This list can be constructed mathematically by listing the ratios of the smallest integers and including their harmonic inverses (defined below). First, list the ratios of the integers from 1 to 5, where the ratios are between 1 (unison) and 2 (octave): 1/1, 2/1, 3/2, 4/3, 5/3, and 5/4. Then include their harmonic inverses [shown in brackets]: 1/1 [2/1], 2/1 [1/1], 3/2 [4/3], 4/3 [3/2], 5/3 [6/5], and 5/4 [8/5]. Remove the duplicates. We can ignore the trivial unison interval. This leaves: 2/1, 3/2, 4/3, 5/3, 5/4, 6/5, and 8/5. If you start with the integers from 1 to 3 or 1 to 4, the result is the top three intervals: 2/1, 3/2, and 4/3. If you start with the integers from 1 to 5 or 1 to 6, the result is this list of seven intervals.
Harmonic inverses: Two intervals are harmonic inverses of each other if they combine to make an octave, in other words, if the ratios multiplied together equals two — for example, 3/2 x 4/3 = 2. Harmonic inverses appear spontaneously when you construct a new musical scale. Imagine making a musical instrument with three strings. Start with two strings making an octave, a low string and a high string with half the length and twice the pitch. Now, add a string somewhere in the middle, for example, 2/3 the length and 3/2 the pitch of the low string. Playing the low and middle strings together makes a 3/2 interval (perfect fifth), and playing the middle and high strings together makes another interval, the harmonic inverse of 3/2, which is 2/(3/2) = 4/3 (perfect fourth). Each time you add a string between the low and high strings (the octave), you always get two intervals that are harmonic inverses.
Originally, people constructed scales based on pure or natural ratios of small integers. For example, the just intonation system uses the exact ratios shown in the table below. However, this method runs into problems for fixed-pitch instruments, especially keyboard instruments but also fretted string instruments and valved or keyed wind instruments. Although some of the intervals are perfect, other combinations of notes sound very bad ("wolf intervals"). After the Middle Ages in Europe, music became more complex, with more polyphony and more key changes, and these bad intervals became more common.
The modern equal temperament (ET) system was invented (in the 1500s) to solve this problem. (Galileo's father, a music theorist, was one early proponent of equal temperament.) The octave is divided into twelve exactly equal intervals. In this system, the smallest interval, the semitone, is not a simple integer ratio, but is the twelfth root of two (21/12) or approximately 1.059. Larger intervals are powers of the twelfth root of two, as shown in the table below. Although no interval (except the octave) is perfect in this system, the error is "spread around" evenly so there are no very bad intervals.
The table below compares just intonation with equal temperament. The intervals in both systems are never exactly the same (except the octave), but they are very close — always within about one percent or better. For example, the fifth (3/2), obtained by multiplying the twelfth root of two by itself seven times, is 1.498 — very nearly a perfect 1.500. The fourth (4/3), obtained by multiplying the twelfth root of two by itself five times, is 1.335 — very nearly a perfect 1.333.
| Number of Semitones |
Interval Name |
Notes | Consonant? | Just Intonation* |
Equal Temperament |
Difference |
|---|---|---|---|---|---|---|
| 0 | unison | C-C | Yes | 1/1=1.000 | 20/12=1.000 | 0.0% |
| 1 | semitone | C-C♯ | No | 16/15=1.067 | 21/12=1.059 | 0.7% |
| 2 | whole tone | C-D | No | 9/8=1.125 | 22/12=1.122 | 0.2% |
| 3 | minor third | C-E♭ | Yes | 6/5=1.200 | 23/12=1.189 | 0.9% |
| 4 | major third | C-E | Yes | 5/4=1.250 | 24/12=1.260 | 0.8% |
| 5 | perfect fourth | C-F | Yes | 4/3=1.333 | 25/12=1.335 | 0.1% |
| 6 | tritone | C-F♯ | No | 7/5=1.400 | 26/12=1.414 | 1.0% |
| 7 | perfect fifth | C-G | Yes | 3/2=1.500 | 27/12=1.498 | 0.1% |
| 8 | minor sixth | C-A♭ | Yes | 8/5=1.600 | 28/12=1.587 | 0.8% |
| 9 | major sixth | C-A | Yes | 5/3=1.667 | 29/12=1.682 | 0.9% |
| 10 | minor seventh | C-B♭ | No | 9/5=1.800 | 210/12=1.782 | 1.0% |
| 11 | major seventh | C-B | No | 15/8=1.875 | 211/12=1.888 | 0.7% |
| 12 | octave | C-C' | Yes | 2/1=2.000 | 212/12=2.000 | 0.0% |
* This table shows one variation of just intonation.
So, back to the original question: Why does the standard scale (in Western music) have twelve notes? We have explained that an equal-tempered scale works better in practice for fixed-pitch instruments than a scale based on pure intervals, but we have not yet explained why we prefer the twelve-tone equal-tempered scale. Why do we not use a ten-tone or twenty-tone equal-tempered scale? Is there something special about twelve?
The answer is: Yes, the twelve-tone equal-tempered scale is remarkable. The nearly perfect intervals seen in the table above are not typical of other equal-tempered scales. Consider the seven basic consonant intervals (described above): 2/1, 3/2, 4/3, 5/3, 5/4, 6/5, and 8/5. We observe:
The twelve-tone equal-tempered scale is the smallest equal-tempered scale that contains all seven of the basic consonant intervals to a good approximation — within one percent.
Furthermore, for the most important intervals, the fifth (3/2) and fourth (4/3), the approximations are better — within about one tenth of one percent.
Let's compare the twelve-tone equal-tempered scale to some other equal-tempered scales.
All equal-tempered scales with 14 tones or fewer, except the twelve-tone scale, contain at most only three of the seven basic consonant intervals (including the octave) within one percent.
Several equal-tempered scales with more than twelve and fewer than 53 tones contain all seven basic consonant intervals within one percent, and some of these contain some intervals that are better than the twelve-tone scale, but they also contain some that are worse. The most important intervals, the fifth (3/2) and fourth (4/3), are usually worse.
- 19-tone ET: The fifth and fourth are worse than in 12-tone ET, but the other basic intervals are better.
- 24-tone ET: All the basic intervals are exactly the same as in 12-tone ET.
- 29-tone ET: The fifth and fourth are slighty better than in 12-tone ET, but all the basic intervals have approximately the same accuracy as in 12-tone ET.
- 31-tone ET: The fifth and fourth are worse than in 12-tone ET, but the other basic intervals are better.
- 34-tone ET: The fifth and fourth are worse than in 12-tone ET, but the other basic intervals are better.
- 41-tone ET: The fifth and fourth have approximately the same accuracy as in 12-tone ET, but the other basic intervals are better.
- 53-tone ET: All seven basic intervals have better accuracy than 12-tone ET.
But bigger is not necessarily better. Although scales with many tones have many nearly pure intervals that are consonant (ratios of small integers), they have even more intervals that are dissonant (not ratios of small integers). In contrast, the small twelve-tone equal-tempered scale has more consonant intervals (seven) than dissonant intervals (five). We observe:
The twelve-tone equal-tempered scale is the only equal-tempered scale that contains all seven of the basic consonant intervals to a good approximation — within one percent — and contains more consonant intervals than dissonant intervals.
Also, scales with many tones are too large to be really practical: a keyboard with the same range as a piano would be huge.
In summary, the twelve-tone equal-tempered scale is probably the best compromise of all possible scales for fixed-pitch instruments, and that is why it is now standard in Western music and common all over the world.
Which equal-tempered scales, other than the twelve-tone scale, are most widely used? We are including here only equal-spaced or roughly equal-spaced scales, not unequal-spaced scales such as the common pentatonic scales (black keys) and heptatonic scales (white keys).
- Roughly equal-spaced 5-tone and 7-tone scales are found in several musical traditions. The Indonesian gamelan slendro scale is a roughly equal-spaced 5-tone scale.
- The 6-tone (whole-tone) equal-tempered scale is sometimes used in Western music, as in the impressionistic music of Debussy.
- The 19-tone equal-tempered scale has been used by some Western musicians since the Renaissance.
- Indian music uses a subset of a roughly equal-spaced 22-tone (22 shruti) scale. (The Western 12 tones can be related to the 22 shrutis as follows, two tones, unison (1) and fifth (3/2), correspond to two basic shrutis, and the remaining ten tones each correspond to a range of tones bounded by two shrutis.)
- Arabic and other Middle Eastern music uses a subset of a roughly equal-spaced 24-tone (quarter-tone) equal-tempered scale. The quarter-tone scale has been used by some Western musicians (Boulez, Ives).
- The 31-tone equal-tempered scale has been used by some Western musicians since the Renaissance, especially in the Netherlands (due to Huygens).
The Equal Temperament Musical Scales Worksheet (MS Excel spreadsheet or PDF document) shows all the ET scales (up to 100 tones) and shows how well they match the "ideal" intervals. If you don't agree with my ideal intervals, the spreadsheet allows you to enter your own ideal intervals. If you don't agree with my scoring, you can change the score function, if you know basic programming.
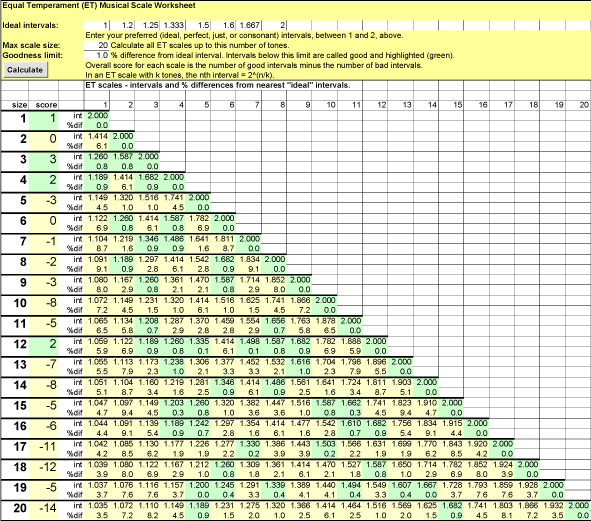
Note: My mathematical results showing the specialness of the twelve-tone scale are fairly robust. When I perform the same analysis with small variations of the discretionary inputs, the twelve-tone scale still looks remarkable. For example, if I add or remove a few intervals near the end of my list of consonant intervals, the results are similar. Also, if I increase the matching tolerance from 1% to 2% or reduce it to 0.8%, the results are similar. You can try your own variations with the spreadsheet above.