Numbers
Real Number Sets
Natural

Natural numbers are the counting numbers {1, 2, 3, ...} (positive integers) or the whole numbers {0, 1, 2, 3, ...} (the non-negative integers). Mathematicians use the term "natural" in both cases.
Integer

Integers are the natural numbers and their negatives {... −3, −2, −1, 0, 1, 2, 3, ...}. (Z is from German Zahl, "number".)
Rational

Rational numbers are the ratios of integers, also called fractions, such as 1/2 = 0.5 or 1/3 = 0.333... Rational decimal expansions end or repeat. (Q is from quotient.)
Real Algebraic

The real subset of the algebraic numbers: the real roots of polynomials. Real algebraic numbers may be rational or irrational. √2 = 1.41421... is irrational. Irrational decimal expansions neither end nor repeat.
Real

Real numbers are all the numbers on the continuous number line with no gaps. Every decimal expansion is a real number. Real numbers may be rational or irrational, and algebraic or non-algebraic (transcendental). π = 3.14159... and e = 2.71828... are transcendental. A transcendental number can be defined by an infinite series.
Real Number Line
Real Number Set Diagram

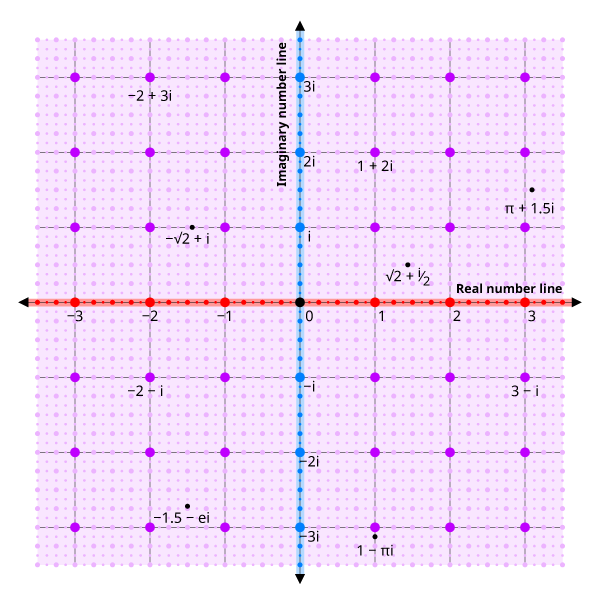
Complex Number Sets
Imaginary
Imaginary numbers are numbers whose squares are negative. They are the square root of minus one, i = √−1, and all real number multiples of i, such as 2i and i√2.
Algebraic

The roots of polynomials, such as ax3 + bx2 + cx + d = 0, with integer (or rational) coefficients. Algebraic numbers may be real, imaginary, or complex. For example, the roots of x2 − 2 = 0 are ±√2, the roots of x2 + 4 = 0 are ±2i, and the roots of x2 −4x +7 = 0 are 2±i√3.
Complex

Complex numbers, such as 2+3i, have the form z = x + iy, where x and y are real numbers. x is called the real part and y is called the imaginary part. The set of complex numbers includes all the other sets of numbers. The real numbers are complex numbers with an imaginary part of zero.
Complex Number Plane
z = x + iy, i = √−1
Complex Number Set Diagram
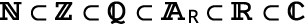
Note: This is an Euler diagram.
Properties of the Number Sets
 |
 |
 |
 |
 |
 |
|
|---|---|---|---|---|---|---|
| Natural | Integer | Rational | Real | Algebraic | Complex | |
| Closed under Addition1 | ● | ● | ● | ● | ● | ● |
| Closed under Multiplication1 | ● | ● | ● | ● | ● | ● |
| Closed under Subtraction1 | ● | ● | ● | ● | ● | |
| Closed under Division1 | ● | ● | ● | ● | ||
| Dense2 | ● | ● | ● | ● | ||
| Complete (Continuous)3 | ● | ● | ||||
| Algebraically Closed4 | ● | ● |
- Closed under addition (multiplication, subtraction, division) means the sum (product, difference, quotient) of any two numbers in the set is also in the set.
- Dense: Between any two numbers there is another number in the set.
- Continuous with no gaps. Every sequence that keeps getting closer together (Cauchy sequence) will converge to a limit in the set.
- Every polynomial with coefficients in the set has a root in the set.
The complex numbers are the algebraic completion of the real numbers. This may explain why they appear so often in the laws of nature.
Infinity
∞
The integers, rational numbers, and algebraic numbers are countably infinite, meaning there is a one-to-one correspondence with the counting numbers. The real numbers and complex numbers are uncountably infinite, as Cantor proved.