thinkzone.wlonk.com

Big Numbers

Some very big numbers

Googol = 10100 =
10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000.
The number of particles in the universe is less than a googol.
(The name "googol" was invented by the 9-year-old nephew of a mathematician.)

100! (100 factorial) = 1 × 2 × 3 × ... × 100 = 9.3326... × 10157 =
93 326 215 443 944 152 681 699 238 856 266 700 490 715 968 264 381 621 468 592 963 895 217 599 993 229 915 608 941 463 976 156 518 286 253 697 920 827 223 758 251 185 210 916 864 000 000 000 000 000 000 000 000.
This is bigger than a googol.
(Can you figure out why 100 factorial ends with 24 zeros?)

Googolplex = 10googol = 1010100.
This is much bigger than a googol.

Skewes' number: In 1933, Stanley Skewes used the number 10101034 in a proof involving prime numbers. G. H. Hardy said it was "the largest number which has ever served any definite purpose in mathematics". Skewes' number is much bigger than a googolplex.

To talk about bigger numbers, we'll need to use new notations that go beyond exponentiation and factorial. The next step is tetration.

Tetration

Multiplication is just repeated addition: for example, 2 × 3 = 2 + 2 + 2. Exponentiation is just repeated multiplication: for example, 23 = 2 × 2 × 2. But, what is repeated exponentiation called? It is called tetration. For example, 2 tetrated to 3, represented as 32, is equal to 222 = 24 = 16. The word "tetration" comes from "tetra" (meaning "four") because it is the fourth operation in this series: addition, multiplication, exponentiation, tetration.

Tetration of even quite small numbers produces very large numbers. This may be why it is not very useful in practice. Scientists almost never use tetration.

Example tetrations:

The next operation beyond tetration is called pentation. Pentation is repeated tetration. You can imagine how big those numbers must be!

Special notations for bigger numbers

To write bigger and bigger numbers, people invent special notations. Here is Knuth's up-arrow (↑) notation:

Reading about these notations is fun and mind-bending. Search for these: Knuth's up-arrow notation, Hyper-operations, Ackermann functions, Steinhaus-Moser notation, Conway's chained arrow notation, Jonathan Bowers' extended operators, and fast-growing hierarchy.

Some extremely big numbers

These numbers are so big that they require special notations.

Graham's number
Graham's number [Martin Gardner]

Graham's number: In 1971, Ronald Graham used an extremely large number in a proof involving combinatorics. Martin Gardner called Graham's number "the largest number ever used in a serious mathematical proof". The Guiness Book of World Records listed it as the largest useful number. Martin Gardner described Graham's number with a 64-layer diagram. It starts at the top with the number 3↑↑↑↑3, using Knuth's arrow notation, already an incomprehensibly large number. That huge number is the number of arrows in the next layer. Repeat until you get to layer 64, which is Graham's number (g64). It is jaw-droppingly huge.

TREE(n): In 2006, Harvey Friedman introduced the function TREE(n), a rapidly-growing sequence involving, you guessed it, trees (based on Kruskal's tree theorem). The first terms are TREE(1)=1 and TREE(2)=3. But then it explodes, TREE(3) is much bigger than Graham's number.

SCG(n), SSCG(n): In 2006, Friedman introduced the functions SCG(n) and SSCG(n), related to subcubic graphs, that grow faster than TREE(n). SCG(3) and SSCG(3) are each much bigger than TREE(3).

The study of extremely large numbers is called googology.

Beyond computable numbers

Bigger still are "non-computable" sequences of numbers.

Be forewarned, the following paragraphs involve some very abstract concepts. I will merely mention these concepts here, not attempt to explain them. I don't fully understand them myself. My only aim is to give you a taste for these huge numbers.

First, you should know that Turing machines (invented by Alan Turing) are theoretical computers that simulate real computers. Each Turing machine has a built-in finite-state computer program and an infinitely long tape. By definition, anything that can be computed may be computed on a Turing machine. Also, you should know that Turing proved that it is sometimes impossible to decide whether a given Turing machine will run forever or eventually halt (this is called the halting problem).

The mathematical operations above, such as tetration, are all computable on a Turing machine. However, there are other well-defined but non-computable sequences of numbers that grow faster than any computable sequence of numbers.

BB(n): In 1962, Tibor Radó introduced the Busy Beaver. A Busy Beaver is a Turing machine that eventually halts but runs for more steps than most other Turing machines of the same number of states. The Busy Beaver function, BB(n), gives the maximum number of steps run by the Busiest Beaver with n states. But only some of these numbers can be determined, because of the undecidablity of the halting problem. The first few Busy Beaver numbers are known: BB(1) = 1, BB(2) = 6, BB(3) = 21, BB(4) = 107, and BB(5) = 47,176,870. BB(6) is known to be huge (> 2↑↑↑5), and it may be non-computable, so mathematicians may never know how big it is!

Rayo(n): In 2007, Augustín Rayo won a big-number contest with a number, now called Rayo's number or Rayo(10100). The function Rayo(n) gives the smallest positive integer bigger than any finite positive integer named by an expression in the language of first-order set theory with n symbols or less. So, Rayo's number, Rayo(10100), is bigger than any number that can be defined with a googol symbols! Of course, the value depends on how you define the language of first-order set theory. The function grows slowly at first (for example, Rayo(n)=0 for n < ~10) but later it grows explosively. It is non-computable. Rayo(n) grows much faster than BB(n). Some other functions that beat Rayo(n) are extensions of Rayo's method.

If you really want to understand these difficult concepts, you'll need to read up on it elsewhere.

Infinity

Georg Cantor showed that there are many levels of infinity: some infinities are larger than other infinities. He defined two infinite sets to be the same size if there is a way to arrange the members of the first set in one-to-one correspondence with the members of the second set. You might expect that the infinity of positive integers {1, 2, 3, ...} to be twice as big as the infinity of even positive integers {2, 4, 6, ...}, but these two infinities are the same size because they can be put in one-to-one correspondence like this: 1 → 2, 2 → 4, 3 → 6, etc.

Cantor proved that the infinity of real numbers is greater than the infinity of integers. The integers are countably infinite, but the real numbers are uncountably infinite. No matter how you try to arrange the real numbers in one-to-one correspondence with the integers, you'll always have more real numbers than integers. Cantor's ingenious "diagonal proof" is short and sweet. Here's the gist of the proof. First, imagine listing all real numbers between 0 and 1 in any order you choose. Number the list with all the positive integers in order, 1, 2, 3, etc.

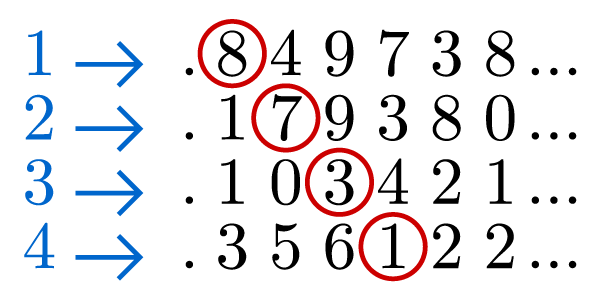
Now construct the real number X by choosing all the digits on the diagonal as shown (X = .8731...). Then construct the real number Y by changing every digit in X to any other digit (for example, Y = .9842...). Y differs from every real number on the list by at least one digit, so Y is a real number that is not on the list. Therefore, the infinity of real numbers must be greater than the infinity of positive integers. To prove it for all integers, positive and negative, simply renumber the list with all integers in this order: 0, 1, -1, 2, -2, 3, -3, etc.

Mathematicians have explored levels of infinity beyond Cantor's infinities.

References