Tomograms

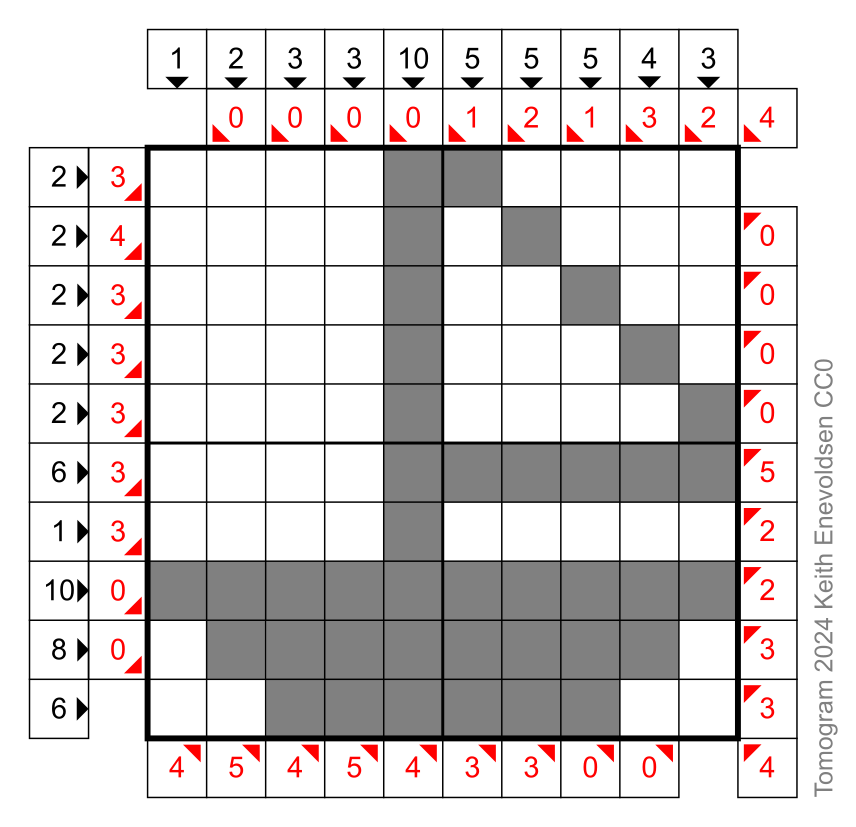
Tomograms are picture logic puzzles. The rules are simple. You are given a grid of cells and the total numbers of filled cells in each row, column, and diagonal. Use logic to fill in the cells and make a picture.

Tomogram puzzle, partially solved — Example, partially solved.

Tomogram puzzle solution: a sailboat. — Example solution: a sailboat.

The outer (black) numbers have arrows pointing to the rows and columns, and the inner (red) numbers have arrows pointing to the diagonals.

A tomogram puzzle is similar to a nonogram puzzle. The differences are that a tomogram includes diagonals, and a tomogram provides only one number per row, column, or diagonal. A tomogram puzzle is similar to a computed tomography (CT) scan. A medical CT scanner computes a cross-section image based on X-ray data from many directions. The word "tomogram" comes from "tomo-" meaning "section" and "-gram" meaning "drawing".

Solving hints

Basic strategy. First, find the rows, columns, and diagonals that must be all filled or all empty. Mark those cells as filled or empty. (You can always immediately determine the four corner cells.) Continue finding the rows, columns, and diagonals in which the remaining unknown cells must be all filled or all empty. Mark those cells as filled or empty.
Completely fill each filled cell. Mark each known empty cell with a dot.
When you complete a row, column, or diagonal, cross off the number.
A straightedge may help you follow the diagonals.
For difficult puzzles, if you get stuck, you may need to guess (suppose or posit) that one or more cells are filled or empty, then follow the consequences of that supposition. For example, a cell at the intersection of several high numbers is more likely to be filled, and a cell at the intersection of several low numbers is more likely to be empty. You may also use the appearance of the emerging picture to make guesses about which cells are likely to be filled or empty. If your guesses turn out to be wrong, you will need to erase your guesses, so use different markings for known and guessed cells.
Checking for symmetry may help. If the picture has symmetry (like a face with bilateral symmetry), the symmetry will be revealed by the patterns of the numbers (can you see how?). If the picture has bilateral symmetry, you can immediately solve all the cells that lie directly on the middle axis of symmetry (can you see how?).

Here are some puzzles for you to print and solve.

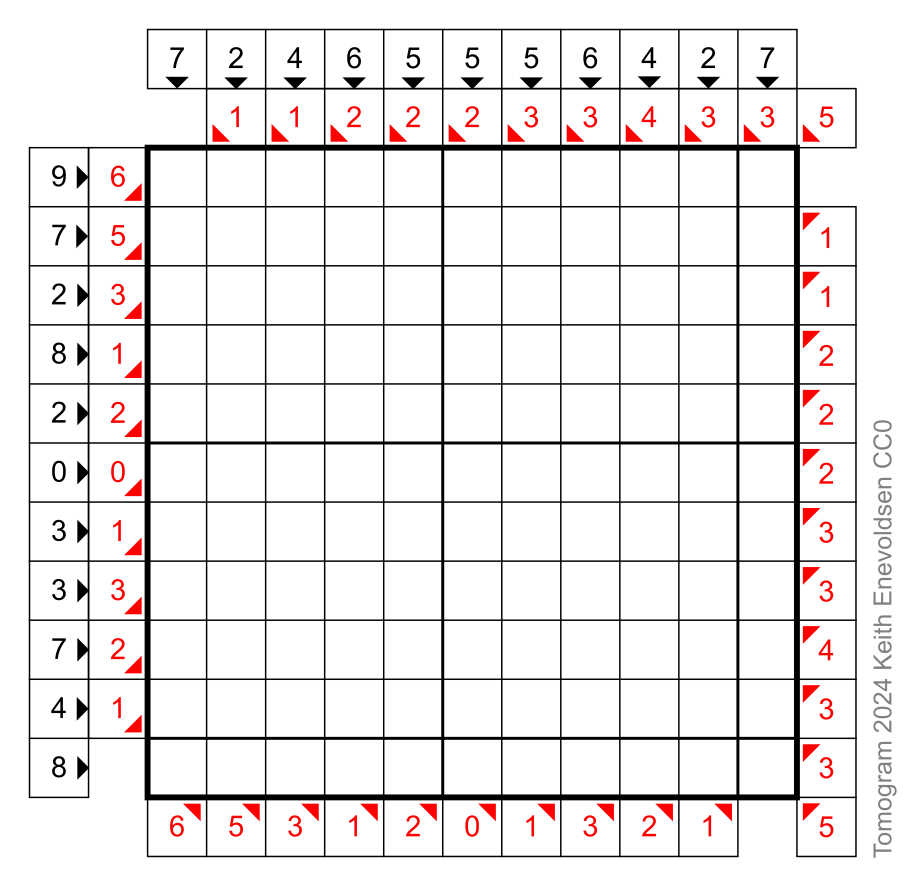
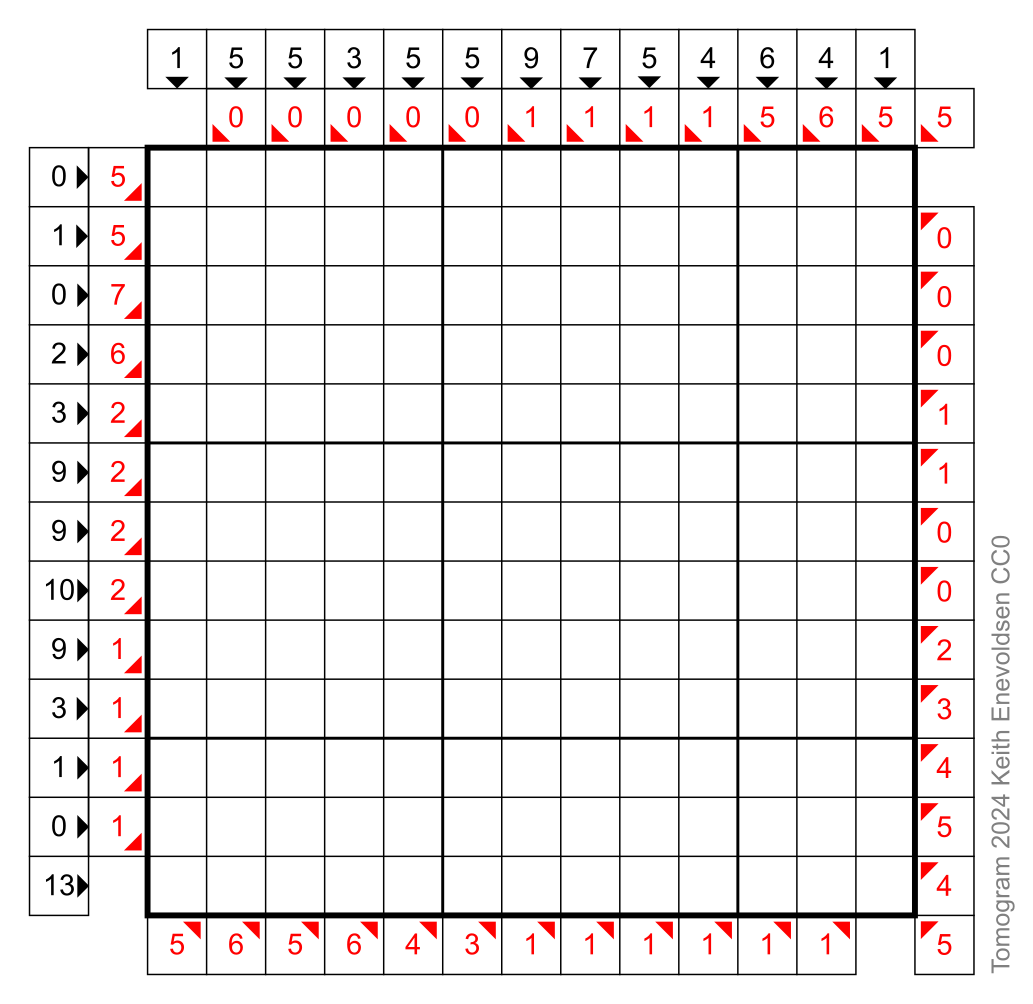
Puzzles marked difficult (★★★) require more than the basic strategy.

Solutions: 10x10-1, 10x10-2, 10x10-3, 11x11-1, 12x12-1, 13x13-1, 14x14-1, 15x15-1, 15x15-2, 15x15-3, 15x15-4, all solutions.

You can make your own tomograms.